其实应该更准确的称为“First Exit Time”问题:我们考虑到一个粒子,其初始位置在![]() 处。每个时刻其向左或向右走
处。每个时刻其向左或向右走![]() 距离,其中
距离,其中![]() 服从均值为
服从均值为![]() ,标准差为
,标准差为![]() 的正态分布,同时在坐标轴上,在
的正态分布,同时在坐标轴上,在![]() 和
和![]() 处各有两个吸收壁,当粒子碰到吸收壁时,即消逝。求随着时间增加,粒子仍然未被吸收的概率密度分布。
处各有两个吸收壁,当粒子碰到吸收壁时,即消逝。求随着时间增加,粒子仍然未被吸收的概率密度分布。
这类问题在电路中也可能会产生应用:考虑一个伪差分的压控振荡器(VCO),其相位差会随着时间的增加而增加,同样也会受到噪声影响,当相位差超过一定范围,就可以触发一个鉴相器输出结果;或者考虑一个积分器对电压或电流采样,每次累加的电压服从一个正态分布,此时若对溢出的时间进行统计,则可以获得采样的电压的信息。
First Exit Time(FET)问题通常可以使用Fokker-Planck Equation方程来描述,这里以一个VCO比较器为例。
考虑一个伪差分VCO比较器,后面接一个鉴相器。设![]() 表示鉴相器的死区大小,正或负的输入电压
表示鉴相器的死区大小,正或负的输入电压![]() 使累积的相位差分别向
使累积的相位差分别向![]() 或
或![]() 漂移(drift)。
漂移(drift)。
设![]() 表示
表示![]() 和
和![]() 之间的瞬态相位差,随机变量
之间的瞬态相位差,随机变量![]() 的概率密度
的概率密度![]() 的Fokker-Planck方程为
的Fokker-Planck方程为
(1) ![]()
为了简化问题的分析,我们假设鉴相器是连续时间工作的,即一旦![]() 超过
超过![]() ,振荡会立即停止,由此可以得到方程的边界条件为
,振荡会立即停止,由此可以得到方程的边界条件为
(2) ![]()
(3) ![]()
其中 ![]() 是迪拉克Delta函数。下面给出方程(1)在边界条件(2)-(3)的解法。
是迪拉克Delta函数。下面给出方程(1)在边界条件(2)-(3)的解法。
一维定边界噪声时间无关的Fokker-Planck的解析解法
为了方便表示,我们将方程(1)和边界条件(2)-(3)重写为以下形式
(4) ![]()
设![]() ,有
,有
(5) ![]()
分离变量
(6) ![]()
(7) ![]()
可得
(8) ![]()
若![]() ,
, ![]() ,
, ![]() ,
, ![]()
(9) ![]()
(10) ![]()
解得![]() ,平凡解。
,平凡解。
若![]() ,
, ![]() ,
, ![]()
(11) ![]()
解得![]() ,平凡解。
,平凡解。
若![]() ,
, ![]() ,
, ![]() ,
, ![]()
(12) ![]()
(13) ![]()
解得
(14) ![]()
(15) ![]()
(16) ![]()
(17) 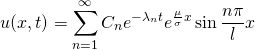
由边界条件
(18) 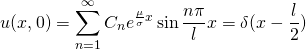
(19) 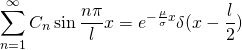
利用固有函数系的正交性可得
(20) 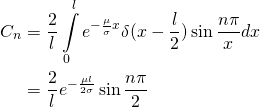
因此,函数的解为
(21) 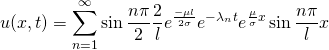
即
(22) 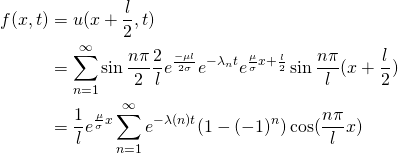
其中![]()
一个利用概率密度函数的例子:简单积分、亚稳态深度
由上一小节,我们可以得到方程(1)的解为
(23) 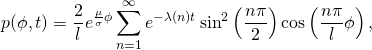
其中
(24) ![]()
公式(23)即描述了在存在噪声的情况下基于闭环VCO的比较器的瞬态行为。
我们可以定义当比较器在一定时间后仍然未能做出决定为一个亚稳态(Metastability)事件,即此时压控振荡器仍在振荡。
设![]() 为
为![]() 个周期后发生亚稳态的概率,则即对上面的概率密度函数进行积分,有
个周期后发生亚稳态的概率,则即对上面的概率密度函数进行积分,有
(25) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} P(k)=&\int_{-l/2}^{l/2}p\left(\phi, \frac{k}{f_0}\right) d\phi\\ =&4\pi\sigma^2\cosh\left(\frac{\mu l}{2\sigma}\right)\sum_{n=1}^{\infty}\left[\frac{ne^{-\lambda\left(n\right)\frac{k}{f_0}}\sin\left(\frac{n\pi}{2}\right)}{\mu^2 l^2+n^2\pi^2\sigma^2}\right]. \end{split} \end{equation*}](https://m0nkey.cn/wp-content/ql-cache/quicklatex.com-4429e39a56d4dbaca33e815727cf036c_l3.png)
Fokker-Planck方程更直觉的理解
可以看出,上面的解析解还是比较复杂的,为了方便直觉理解,我们重新在没有边界条件(3)的情况下解方程(1),那么得到的结果就非常直接明了了:
(26) 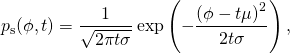
这个结果,即高斯分布的概率密度函数,均值![]() 和方差
和方差![]() 随着时间线性增加。这其实就是一个一维维纳过程(Wiener Process)。
随着时间线性增加。这其实就是一个一维维纳过程(Wiener Process)。
延伸思考
- 在添加了吸收壁的情况下,函数的概率密度函数就从维纳过程变成了复杂的无穷级数。在工程应用中,一定条件下可以用维纳过程来减少复杂度,帮助理解。
- 如果吸收壁是可移动的,系统的模型会更复杂,但是会不会有更好的效果:更低的亚稳态概率,或者更低的噪声。
相关阅读
- 一维随机游走,带移动吸收壁,吸收的期望时间是否有限?https://www.zhihu.com/question/36413595/answer/67866180
- Markov 链与 Fokker-Planck 方程有什么内在联系?https://www.zhihu.com/question/63553355